Quantum Chemistry tutorial

Finding the conical intersection between the excited and ground state in a protonated schiff base with Gaussian09.

Introduction

In one of the previous lecture we've learned about the conical intersections. At such intersections, the adiabatic surfaces touch. We have seen that the degeneracy between the electronic states is lifted (to first order) by displacements in so-called branching space. In the remaining (3N-8) internal degrees of freedom, the degeneracy can be maintained, forming a 3N-8 dimensional seam. In this tutorial we will locate the minimum energy point on this seam, the so called minimum energy conical intersection (MECI). The package we are going to use is called Gaussian. It is among the modern electronic structure codes available and provides an easy-to-use interface called Gaussview that allows for a user-friendly access to quantum chemistry.

To learn how to use the program by yourself or maybe extend your knowledge beyond the scope of this tutorial one can check out the links on the following site.

To start a calculation we basically need four things:

With these options determined, Gaussian can compute the electronic wave function. With the wave function at hand, we have access also to the energy and energy gradients with respect to nuclear displacement. With the latter we can search for stationary points, at which these gradients are zero.

In this practical we will locate the minimum energy conical intersection. At this point, the energy gap in the branching space space is zero, while the gradients in the 3N-8 dimensional seam space are zero as well. We will not go into details about the optimization algorithm that we will use to optimize the MECI, but details can be found in Bearpark et al. Chem. Phys. Lett. 223 (1994) 269.

The files needed for this practical can be downloaded as an archive here and unpacked by typing

tar xzvf conical.tar.gz
However, we will try to do everything by ourselves, starting by creating the formaldimine molecule in Gaussview.

Building the molecule

Open gaussview by typing 

gview.exe
This will open a user interface.

Click on the R (fragment) symbol button and select an ethene unit (6th element in top row).

Select the window with the blue background and click in it.

You will see a ethene molecule there now.

Select the main window and click on the the element buttom and select a bare nitrogen atom.

Now select the window in which the ethene is waiting and click on one of the carbon atoms. This atom should become a nitrogen.

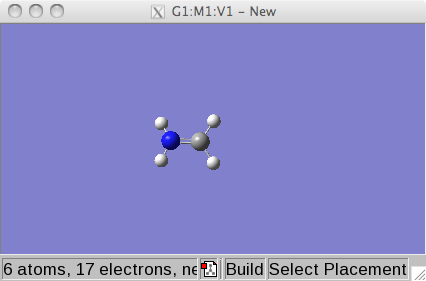
Now we have the starting structure for our purposes and we will start by optimizing its geometry in the electronic ground state in the next step.

Ground state geometry optimization

To model the electronic wave function we will use the complete active space self-consistent field (CASSCF) approach, a multi-configurational method (i.e. wave function is expanded in a limited number of configuration state functions) that will be discussed in detail in one of the lectures. For now it is sufficient to know that with this methods we have access to both ground and excited state wave functions. Fortunately, the molecule is so simple that we need not to worry about selecting the orbitals for the CASSCF computations. We take the HOMO and LUMO, the bonding and anti-bonding pi orbitals, respectively. The electronic transition will promote an elecron from the bonding into the anti-bonding pi orbitals.

We will use Pople's 6-31G basis set to expand the molecular orbitals in. G stands for "Gaussian", so a GTO basis with 6 gaussian functions for the inner (non-valence) electrons and 4 (3+1) for the valence electrons is used.

From the menu in the main window in gaussview, select from the menu the Calculate item.

From the drop down list choose Gaussian Calculation Setup. This opens an interface in which we can setup the calculations

For the geometry optimization at the CASSCF level with 2 electrons in 2 orbitals, which are expanded in the 6-31G basisset, we need to configure the tabs as follows:

Job Type

Next, click the Method tab. Select the Link 0 tab. Here we can select how much memory, how many processors we wish to use, and set the names of output files. We will need a checkpoint file to visualize orbitals with gaussview (optional). Click Retain to store the setup parameters. Now select the main window and choose the file tab and save the file. Again, invent your own filename. I used im.com. The saved file should look something like: 

%chk=/home/gegroenh/im_S0.chk 
# opt casscf(2,2)/6-31g geom=connectivity

Title Card Required

1 1
 C                 -1.86956513    1.60869563    0.00000000
 H                 -2.46315013    2.53273363    0.00000000
 H                 -2.46318113    0.68468163   -0.00002200
 H                  0.04993587    0.68465763   -0.00001900
 H                  0.04996687    2.53270963    0.00002600
 N                 -0.54364913    1.60869563    0.00000000

 1 2 1.0 3 1.0 6 2.0
 2
 3
 4 6 1.0
 5 6 1.0
 6
Now we start the optimization by typing 
g09 im.com
This will take a while. During the calculation Gaussian writes an output file (.log) that communicates the most important infos to the user.

After the calculation is complete, you can open the output .log or .chk in gaussian. Click on the file tab in the main gaussview window and choose open file and select the im.log file.

Next, we want to understand what happens if this molecule absorbs a photon.

Electronic transition to first excited state

To obtain the so-called vertical excitation energy we will do a single point (energy only) computation of the excited state. In a vertical excitation, the nuclei are not allowed to relax during the excitation, which is usually a good approximation for an on-resonance optical excitation. Exciting from the ground state geometry thus brings the system instantly to a point on the excited state energy surface, known as the Franck Condon point. Because the electron distribution is different in the excited state, the Frank Condon point is not a (local) minimum on the excited state potential energy surface.

Take the optimized ground state structure by opening the .log or.chk file of the previous geometry optimization. From the menu in the main window in Gaussview, select Calculate item again and choose Gaussian Calculation Setup. Job Type

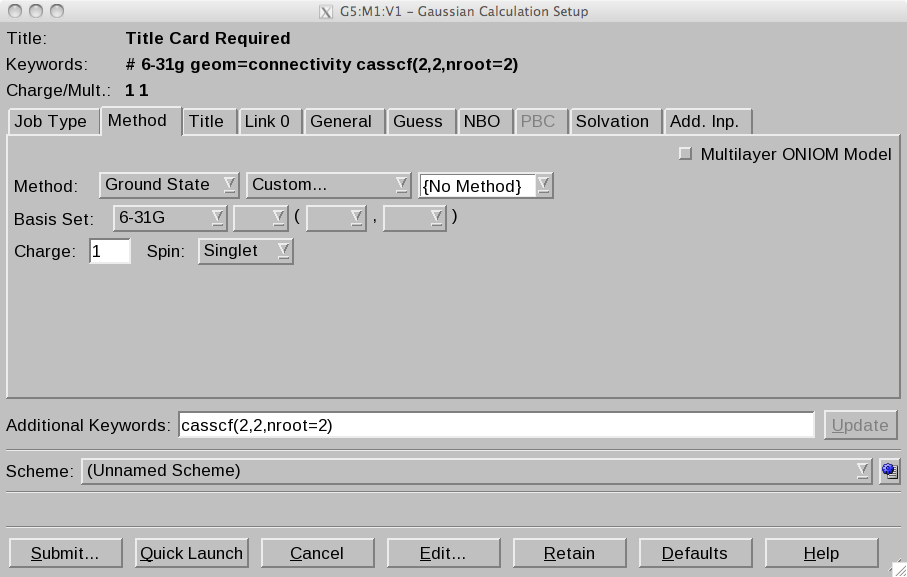
Next, click the Method tab. Because Gaussview does not allow to setup an excited state CASSCF calculations, we do this by hand. We use the Additional Keywords string. Add

Select the Link 0 tab.

This way we request again a CASSCF computations with 2 electrons in two orbitals (HOMO and LUMO), but in contast to the first step, require that the 2nd root of the Configuration Interaction problem is computed, which is the first singlet excited state of this system.

Click Retain to store the setup parameters. Now select the main window and choose the file tab and save the file. Again, invent your own filename. I used im_S1.com. The saved file should look like: 

%chk=/home/gegroenh/im_S1.chk # 6-31g geom=connectivity
casscf(2,2,nroot=2)

Title Card Required

1 1
 C                 -0.67850745    0.00000000    0.00000214
 H                 -1.21382920   -0.92768533   -0.00000877
 H                 -1.21382929    0.92768533    0.00002371
 H                  1.13693295    0.85144265    0.00001049
 H                  1.13693288   -0.85144264   -0.00002024
 N                  0.60354820    0.00000000   -0.00000258

 1 2 1.0 3 1.0 6 2.0
 2
 3
 4 6 1.0
 5 6 1.0
 6
Now we perform the computation by typing 
g09 im_S1.com
What is the excitation energy? What is the excitation wavelength?

Have a look at the orbitals as well. You need to open the .chk file and click on the orbital button. This opens a new window. Here, you first need to render the orbitals in the tab. Then you can select the orbitals in the right window.

What kind of orbitals are these?

Conical intersection between excited and ground state potential energy surfaces

Next we locate the lowest energy conical intersection. As gaussview does not allow one to set up such calculation automatically, we will provide some non-default input parameters by hand. In addition we will tweak the starting structure somewhat in order to speed up the optimization. We will twist around the central N=C double bond to bring the geometry closer to the MECI.

From the main gaussview window open the log or chk file of the previous excited state energy calculation.

Then, select the main window and click the torsion-manipulation button.

Click four atoms that define the torsion (or dihedral) angle around the double bond.

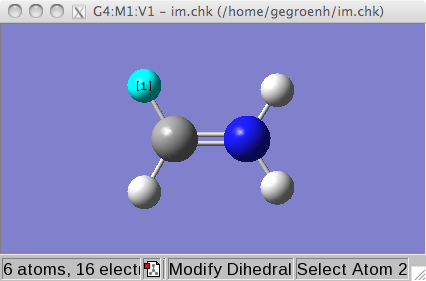
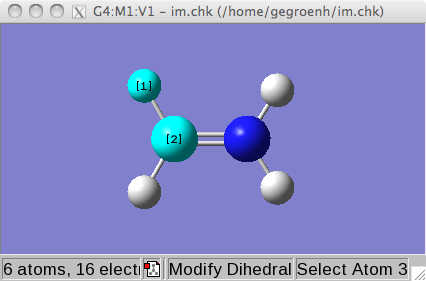
After selecting the fourth atom, a slider window opens.

With the slider you can change to central torsion angle. Set it around 45 degrees.

We will now setup the calculations. Open the Gaussian Calculation Setup window again.

Job Type

Method Because gaussview does not allow to setup an excited state CASSCF calculations, we do this by hand. We also need to state that we want to optimize a conical intersection. We use again the Additional Keywords string. Add

Select the Link 0 tab.

Save the file. The content of this file should look like: 
%chk=/home/gegroenh/im_CI.chk
# 6-31g geom=connectivity casscf(2,2,nroot=2) opt=conical

Title Card Required

1 1
 C                 -0.67850745    0.00000000    0.00000214
 H                 -1.21382862   -0.91434259    0.15677690
 H                 -1.21382987    0.91434372   -0.15676205
 H                  1.13693348    0.83919195    0.14391019
 H                  1.13693235   -0.83919183   -0.14391993
 N                  0.60354820    0.00000000   -0.00000258

 1 2 1.0 3 1.0 6 2.0
 2
 3
 4 6 1.0
 5 6 1.0
 6
Perform the optimization by typing 
g09 im_CI.com
This may take a while. If there are convergence problems in the CASSCF cycles, you may try to add another keyword to the keyword list: iop(5/7=512). This keyword increases the maximum number of SCF cycles in the CASSCF calculation from the default value of 64 to 512. Usually problems in CASSCF convergence hint at problems with the orbitals and/or geometry, so use it with care. Before increases the maximum, make sure to inspect the geometry and orbitals.

What is the energy of the twisted structure? How much is it compared to the FC point? How large is the energy gap between the excited and ground state at the conical intersection?

Open the log file with a viewer, such as less or emacs. Scroll to the last MSCSF cycle. Gaussian prints information about the branching space vectors, the gradient difference vector and derivative coupling vectors. Only displacements along these (cartesian) vectors can lift the degeneracy. When projected onto the 2D subspace spanned by these vectors, the adiabatic surfaces look like a double cone touching at the conical intersection. The vectors can be visualized as shown here.

Gradient difference vector

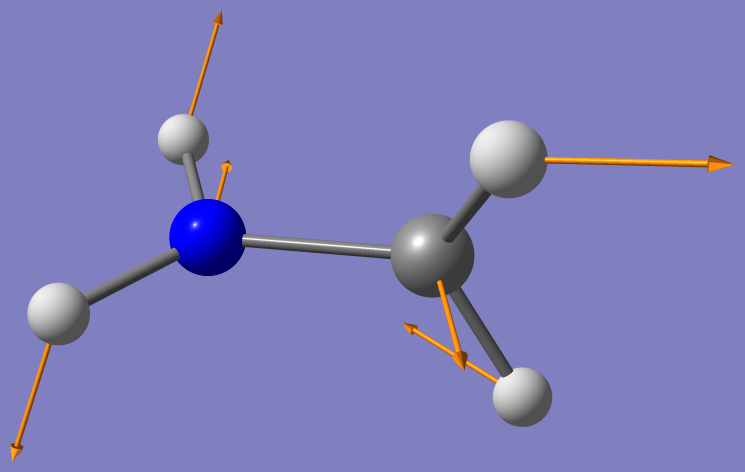
Derivative Coupling vector

Since the enery of the conical intersection is lower, the system can access the conical intersection and decay to the ground state. Since the twisted structure has a higher energy structure on ground state than the minimum energy geometry (by how much? Hint: at the CI the ground and excited state are degenerate), a photon absorption can thus help to bring about an isomerization.

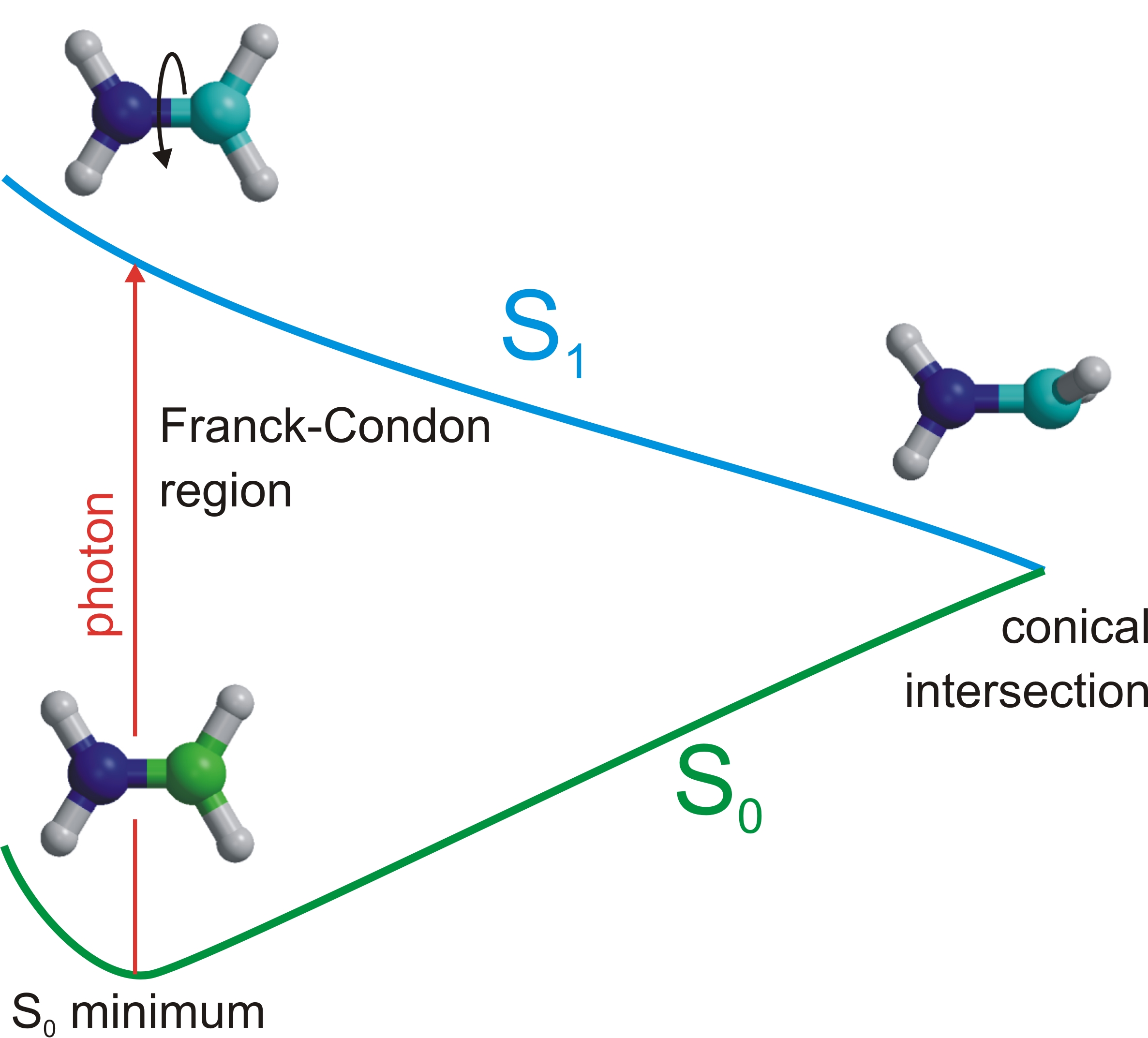
In this exercise there is no chemical difference between the cis and trans isomers. To keep track of the isomerization you can substitute one of the protons on the nitrogen and one of the protons on the carbon by methyl groups and repeat the exercise (optional).